Structure of intersection graphs
Abstract
Let G be a finite group and let N be a fixed normal subgroup of G. In this paper, a new kind of graph on G, namely the intersection graph is defined and studied. We use 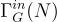 to denote this graph, with its vertices are all normal subgroups of G and two distinct vertices are adjacent if their intersection in N. We show some properties of this graph. For instance, the intersection graph is a simple connected with diameter at most two. Furthermore we give the graph structure of
to denote this graph, with its vertices are all normal subgroups of G and two distinct vertices are adjacent if their intersection in N. We show some properties of this graph. For instance, the intersection graph is a simple connected with diameter at most two. Furthermore we give the graph structure of .png) for some finite groups such as the symmetric, dihedral, special linear group, quaternion and cyclic groups.
for some finite groups such as the symmetric, dihedral, special linear group, quaternion and cyclic groups.
Keywords
Full Text:
PDFDOI: http://dx.doi.org/10.19184/ijc.2021.5.2.6
References
Tong-Viet, Hung P, Finite groups whose prime graphs are regular, J. Algebra, 397 (2014), 18-31.
Kurzweil, Hans and Stellmacher, Bernd, The theory of finite groups: an introduction, Springer Science & Business Media, (2006).
Wilson, Robin J, Introduction to graph theory, Pearson Education India, (1979).
Erfanian, Ahmad and Tolue, Behnaz, Conjugate graphs of finite groups, Discrete Math. Algorithms Appl., 4(02), (2012).
Hai, Zhang Qin and Ji, Cao Jian, Finite groups whose nontrivial normal subgroups have the same order, J. Math. Res. Exp., 28(4), (2008), 807-812.
Refbacks
- There are currently no refbacks.

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.












